Goldbeter-Koshland kinetics
The Goldbeter-Koshland kinetics describe a steady-state solution for a 2-state biological system. In this system, the interconversion between these two states is performed by two enzymes with opposing effect. One example would be a protein Z that exists in a phosphorylated form ZP and in an unphosphorylated form Z; the corresponding kinase Y and phosphatase X interconvert the two forms. In this case we would be interested in the equilibrium concentration of the protein Z (Goldbeter-Koshland kinetics only describe equilibrium properties, thus no dynamics can be modeled). It has many applications in the description of biological systems.
The Goldbeter-Koshland kinetics is described by the Goldbeter-Koshland function:
with the constants
Graphically the function takes values between 0 and 1 and has a sigmoid behavior. The smaller the parameters J1 and J2 the steeper the function gets and the more of a switch-like behavior is observed.
Derivation
Since we are looking at equilibrium properties we can write
From Michaelis–Menten kinetics we know that the rate at which ZP is dephosphorylated is ![r_1 = \frac{k_1 [X] [Z_P]}{K_{M1}%2B [Z_P]}](/2012-wikipedia_en_all_nopic_01_2012/I/e46a80b4f7c77d7a571a14fc6917ad3c.png) and the rate at which Z is phosphorylated is
and the rate at which Z is phosphorylated is ![r_2 = \frac{k_2 [Y] [Z]}{K_{M2}%2B [Z]}](/2012-wikipedia_en_all_nopic_01_2012/I/70f89ed91892ee01ce002322e8d96643.png) . Here the KM stand for the Michaelis Menten constant which describes how well the enzymes X and Y bind and catalyze the conversion whereas the kinetic parameters k1 and k2 denote the rate constants for the catalyzed reactions. Assuming that the total concentration of Z is constant we can additionally write that [Z]0 = [ZP] + [Z] and we thus get:
. Here the KM stand for the Michaelis Menten constant which describes how well the enzymes X and Y bind and catalyze the conversion whereas the kinetic parameters k1 and k2 denote the rate constants for the catalyzed reactions. Assuming that the total concentration of Z is constant we can additionally write that [Z]0 = [ZP] + [Z] and we thus get:
with the constants
If we thus solve the quadratic equation (1) for z we get:
Thus (3) is a solution to the initial equilibrium problem and describes the equilibrium concentration of [Z] and [ZP] as a function of the kinetic parameters of the phoshorylation and dephoshorylation reaction and the concentrations of the kinase and phosphotase. The solution is the Goldbeter-Koshland function with the constants from (2):
Literature
- Goldbeter A, Koshland DE (November 1981). "An amplified sensitivity arising from covalent modification in biological systems". Proc. Natl. Acad. Sci. U.S.A. 78 (11): 6840–4. doi:10.1073/pnas.78.11.6840. PMC 349147. PMID 6947258. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=349147.
- Zoltan Szallasi, Jörg Stelling, Vipul Periwal: System Modeling in Cellular Biology. The MIT Press. p 108. ISBN 978-0262195485
|
|||||||||||
![\begin{align}
z = \frac{[Z]}{[Z]_0 } = G(v_1, v_2, J_1, J_2) &= \frac{ 2 v_1 J_2}{B %2B \sqrt{B^2 - 4 (v_2 - v_1) v_1 J_2}}\\
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/f13612fc0f6203ff51ae69445b3ebf3f.png)
![\begin{align}
v_1 = k_1 [X]�; \
v_2 &= k_2 [Y]�; \
J_1 = \frac{K_{M1}}{[Z]_0 }�; \
J_2 = \frac{K_{M2}}{[Z]_0 }; \
B = v_2 - v_1 %2B J_1 v_2 %2B J_2 v_1
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/f5cab71a63d18c838fa9ecf15d817b00.png)
![\begin{align}
\frac{d[Z]}{dt} \ \stackrel{!}{=}\ 0
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/0299878483fa5fd213a9d0bbeb04099b.png)
![\begin{align}
\frac{d[Z]}{dt} = r_1 - r_2 = \frac{k_1 [X] ([Z]_0 - [Z])}{K_{M1}%2B ([Z]_0 - [Z])} &-\frac{k_2 [Y] [Z]}{K_{M2}%2B [Z]} = 0 \\
\frac{k_1 [X] ([Z]_0 - [Z])}{K_{M1}%2B ([Z]_0 - [Z])} &= \frac{k_2 [Y] [Z]}{K_{M2}%2B [Z]} \\
\frac{k_1 [X] (1- \frac{[Z]}{[Z]_0 })}{\frac{K_{M1}}{[Z]_0 }%2B (1 - \frac{[Z]}{[Z]_0 })} &= \frac{k_2 [Y] \frac{[Z]}{[Z]_0 }}{\frac{K_{M2}}{[Z]_0 }%2B \frac{[Z]}{[Z]_0 }} \\
\frac{v_1 (1- z)}{J_1%2B (1 - z)} &= \frac{v_2 z}{J_2%2B z} \qquad \qquad (1)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/1f3fe9409f949aa5256ba6242725d790.png)
![\begin{align}
z = \frac{[Z]}{[Z]_0 }�; \
v_1 = k_1 [X]�; \
v_2 &= k_2 [Y]�; \
J_1 = \frac{K_{M1}}{[Z]_0 }�; \
J_2 = \frac{K_{M2}}{[Z]_0 }; \ \qquad \qquad (2)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/a0303fafd3e2ef9251ed2a0ca0ec33b7.png)
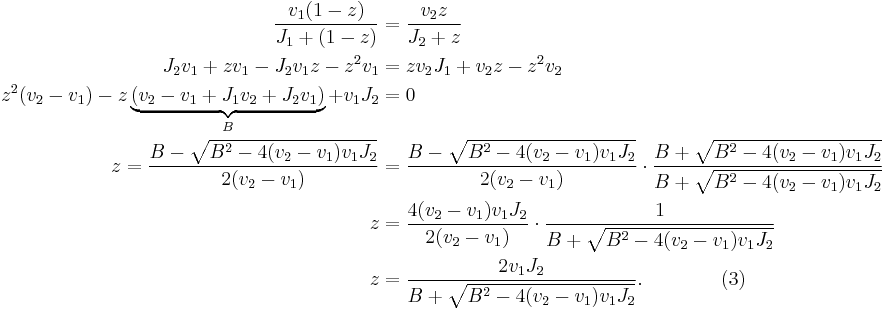
![\begin{align}
z = \frac{[Z]}{[Z]_0 } = G(v_1, v_2, J_1, J_2) &= \frac{ 2 v_1 J_2}{B %2B \sqrt{B^2 - 4 (v_2 - v_1) v_1 J_2}}.\\
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/6b259423802bb9fa56e37215a99aba19.png)